企画担当者にとってよく行う調査にアンケートがあります。
その中で、サンプル数の設定はよくある悩みの種です。
サンプル数が少ないと調査の信頼性が下がり、サンプル数が多いとコストが跳ね上がってきます。
ここでは、アンケートを実施する際の適切なサンプル数の設定について解説していきます。

(2020年7月6日追記)選挙で開票がはじまっていない、もしくははじまって間もないのに「当確」報道が出ることが珍しくありません。
これは、統計学的には「400」のサンプルを取得すれば、概ね全体像を把握することができるからです。
「16,000」まで集まれば、ほぼほぼ誤差がなく正解も出せます。
とりあえず結論だけ知りたい人向け
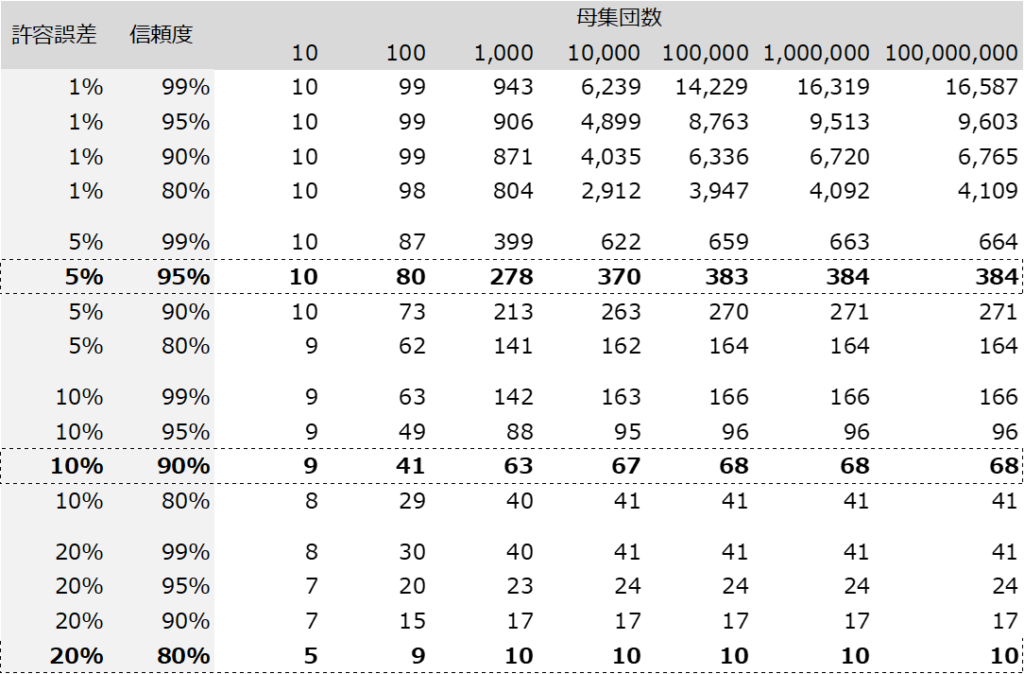
母集団の総数が10,000を超える場合、サンプル数の目安は「400」です。
「400」集まれば十分、と考えて下さい。
なお、母集団の総数が1,000程度の場合は「300」、
100程度の場合は「100」、
10程度の場合は「10」、つまり全調査が必要になります。
用語の意味等、諸々理解されている方は、こちらを見てください。
基本的な用語
ここから、その根拠を理解するための必要な用語知識や計算について解説していきます。
母集団:ターゲットとなる対象の集団全体のこと
母集団数:母集団の対象総数のこと
サンプリング調査:母集団の中から何人かをピックアップして母集団全体の状況を見る調査のこと
サンプル数(サンプルサイズ):サンプリング調査におけるピックアップする対象数のこと
許容誤差:母集団からどの位のズレがあるのかの可能性を示す指標
例えば、許容誤差5%の設定で、ある事象への好感度が70%だとした場合、その「ある事象への好感度」は「65%~75%」ということになります。
ようは、アンケートからえられた結果が「どれだけ実態からかけ離れているか」を示します。
アンケートの目的にもよるのですが、通常は許容誤差5%が設定されます。
信頼度:えられたサンプルが、どれくらいの確率で許容誤差内の結果におさまるのかを示す指標
例えば、信頼度95%の設定で、回答者数が100人、上記の許容誤差5%、ある事象への好感度が70%の場合、「100人中95人」は「ある事象への好感度が65%~75%」ということになります。
アンケートの目的にもよるのですが、通常は信頼度95%が設定されます。
なお、信頼度は許容誤差以上に、必要なサンプル数に与える影響度(感度)が大きいので、無理に高めようとする場合には、よく検討が必要です。
回答率:特定の回答を選択するサンプルの比率のこと
例えば、上記の「ある事象への好感度が70%」の場合は、回答率は70%が設定されます。
ようは、ある程度、回答の傾向がわかっている場合は、必要なサンプル数が減るのです。
ただ、回答傾向は設問内容やターゲットによって変わりますし、基本的には結果がわからない前提でいるはずなので、通常は回答率50%を設定します。
こんな適当な設定でよいのか疑問に思われるかもしれませんが、サンプル数の計算の関係上、50%を設定すると、必要なサンプル数が最大になるため、最も保守的な設定になるのです。
回収率:アンケートを実施した際の回収率のこと、必要なアンケート数に影響する
例えば、不特定多数のアンケートをお願いして戻ってくる想定が10%(10人に1人が回答する)とした場合で、必要なサンプル数が400人なら、4,000人にアンケートを依頼する必要があります。
計算式について
さて、ここで必要なサンプル数を求める計算式を提示します。
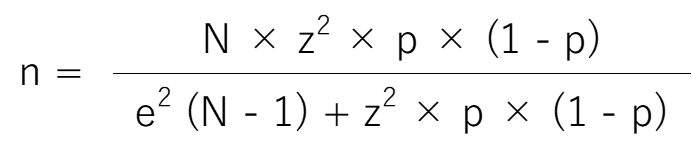
それぞれの意味は下記のとおりです。
数値を代入していけば、サンプル数(n)が求められます。
- n : 必要なサンプル数
- N : 母集団数
- z : 信頼度(Zスコアというものをあてはめます。)
- e : 許容誤差(%での計算なので小数点で計算します、5%なら0.05です。)
- p : 回答率(%での計算なので小数点で計算します、50%なら0.5です。)
ここで信頼度(z)について簡単に触れます。
zスコアは信頼度の%そのままではなく、統計的に対応する数字をあてはめることになります。
統計学のt分布の自由度∞の数字で、信頼度95%なら1.96、信頼度99%なら2.58というように、一律で決定されます。
参考として、末尾にzスコア一覧を掲載しておきます。
具体的に計算してみましょう。
母集団数Nを10,000、信頼度zに1.96、許容誤差eに0.05、回答率pに0.5と設定し、上記の式にあてはめると、369.9837,,,となるはずです。
つまり小数点以下を四捨五入して、「370」です。
ただ、これを一々計算していては身がもたないので、冒頭でも掲示した、このような必要サンプル数の一覧表を見るのが一般的です。

これを見ればわかると思うのですが、許容誤差や信頼度について、精度を高めようと思えば思うほど、必要なサンプル数が一気に増えてしまいます。
そのため、多くの研究やビジネスの現場では、一定水準で精度を確保しつつ、リーズナブルにできる許容誤差5%、信頼度95%、という数字を設定して計算するのです。
逆に考えると、ざっくりと市況感やニーズ感を掴みたい、というのであれば大幅に必要なサンプル数を減らすことができます。
許容誤差10%、信頼度90で設定すれば、サンプル数「100」もあれば、十分以上に知りたいことの概観を掴むことができます。
具体的な検討ステップ
ここからは、より具体的なサンプル数の算出ステップに関して解説していきます。
¶ 母集団数の設定:母集団の規模はどの程度の大きさなのか?
最初のステップが「母集団数の設定」です。
例えば、福利厚生のサービスを提供している日本の会社において、世の中の労働者にとっての福利厚生へのニーズを調査したいとします。
この場合は母集団としては日本の雇用者となります。
数としては雇用者数全体となり、約6,000万人が母集団数となります。
これは就業者数の中の雇用者数全体となるので、より福利厚生を意識するであろう正社員に限定したい場合は、約3,500万人が母集団数となります。
¶ 目的の設定:どの程度の正確性(誤差と信頼度)を要求するのか?
次のステップが正確性、精度の設定、よりかみ砕きつつ正確に言うと、目的の設定です。
調査の目的が、ざっくり粗々にニーズ感を掴みたいのか、それとも具体的なサービスが既にあってそれに対しての情報が欲しいのか、新規事業があって精度高く設定価格の情報をえたいのか、このような形で、どれくらいの正確性、精度を調査に求めるのかを考えます。
ここで上述の通り、許容誤差と信頼度を設定する形になります。
ここのパラメータを個別に検討することには(こういうと統計の専門家からは怒られるかもしれませんが)あまり意味がありません。
ですのでざっくりと3パターン位で考えるのが良いです。
サンプル数は母集団10,000で考えています。
精度重視:許容誤差5%、信頼度95%(サンプル数約400)
標準調査:許容誤差5%~10%、信頼度95%~90%(サンプル数約70~400)
ざっくり:許容誤差10%~20%、信頼度90%~80%(サンプル数約10~70)
許容誤差と信頼度を設定できたら、回答率は50%で設定すればよいので、そのまま必要サンプル数を算出できます。
¶ アンケート依頼数の計算:どういった対象に依頼し回収していくのか?
最後に、どれだけのどういった対象にアンケートを依頼すれば良いのか?の話になります。
アンケート調査代行会社に依頼するのならば、シンプルに「必要サンプル数は400」と伝えれば良いでしょう。
自社でアンケートを実施する場合は、依頼対象との関係性で回収率も変わるので、依頼数が大きく変わります。
必要サンプル数が400で、回収率が20%であるならば、必要依頼数は2,000になります。
アンケート対象が少数ならば、追いかけも可能ですが、100も超えれば現実的には追いかけが困難になります。
ですので、回収率は10%~20%のレンジ内で堅実に設定するのが良いでしょう。
(参考)AIの導入にあたって、何故、膨大なデータ必要なのか?
AIは、ざっくり言うと、過去の膨大な統計データをもとに、ある何かの事象を自動で判定するものです。
上で提示した通り、アンケートによってえられた結果には、誤差があり、かつ信頼レベルも設定されています。
つまり、精度という観点では、あまり質が高くないのです。
現実の研究やビジネスの中では、そこまでの精度を求めてはいないので、必要なサンプル数の中で検証をしていくわけですが、AIにおいては限られたサンプル数(教師データ)では問題がおきます。
というのも、仮にトータルとしての精度を99%にまで高められたとしても、試行100回につき1回は誤った出力をしてしまうのです。
業務内容にもよるのですが、これでは安心して自動化にAIを組み込むことができません。
そのため、膨大な統計データを用意し、トータルとしての精度を99.99,,,と高めて運用する形になります。
(もしくは、素直に精度が低い前提で業務に組み込みます。どちらかというと、こちらの方が現在の主流ですね。)
(参考)信頼度にあてはめるzスコア一覧
| 信頼度 | zスコア |
| 99.9% | 3.290 |
| 99.8% | 3.090 |
| 99.0% | 2.576 |
| 98.0% | 2.326 |
| 95.0% | 1.960 |
| 90.0% | 1.645 |
| 80.0% | 1.282 |
| 70.0% | 1.036 |
| 60.0% | 0.842 |
| 50.0% | 0.674 |




コメント