限界利益を出したい時、損益分岐点分析を行いたい時。
悩ましいのが個変分解です。
今回は、Excelで簡便的に個変分解を行う方法を紹介します。
いわゆる回帰分析法により行います。
用意したサンプルPL
そもそも限界利益とか損益分岐点とかがわからん、という方はこちらの記事を参照してください。
今回は、上記記事で触れた回帰分析法による個変分解を、Excelでやってみましょう、という話です。
用意したサンプルPLは次のようなものです。

これの内、売上高をx(エックス)、営業利益をy(ワイ)として、y = ax + b の数式を、Excelの機能で算出します。
使用する関数紹介(SLOPE関数、INTERCEPT関数)
使用する関数はSLOPE関数とINTERCEPT関数の2つです。
SLOPE関数は、回帰直線の傾きを求める関数です。
SLOPE(yの範囲,xの範囲)で式の入力とセルの選択を行います。
yの範囲およびxの範囲は、それぞれ既知の値をセル範囲または配列で指定します。
INTERCEPT関数は、回帰直線の切片を求める関数です。
INTERCEPT(yの範囲,xの範囲)で式の入力とセルの選択を行います。
こちらも、yの範囲およびxの範囲は、それぞれ既知の値をセル範囲または配列で指定します。
(もし、そもそもy=ax+bとか、傾き・切片とかがわからなければ、中学数学を勉強してみましょう!)
実際の具体を見た方がわかりやすいと思うので、これから提示します。
関数を用いて傾きと切片を求めてみる
冒頭で提示したサンプルPLに、上で紹介した関数を適用してみます。

まずはSLOPE関数です。
適当なセルに下記図のようなイメージで入力とセル選択を行います。

INTERCEPT関数も同様ですね。
適当なセルに下記図のようなイメージで入力とセル選択を行います。

これにより算出した結果が下記図です。

y = 0.73x – 5,297 という結果が出ました。
この計算式を元に、個変分解後のPLを算出したのが次のPL図です。

元のPLと比較しても、精度高く計算できている事がわかりますね。

このような形で、Excelの関数を用いると、簡単に個変分解を行う事ができます。
(もちろん、会社のPLは複雑なので、ここまでキレイな結果が出る事は稀ですが、シンプルなPLですとかなり精度高く出す事ができます。)
グラフから算出する方法もある
今度は関数を用いずにグラフから算出する方法も紹介します。
元のPLの内、X部分とY部分を選択します(わかりやすい様に色を黄色に変えています)。

そして、Excelのタブの内「挿入」タブを選択。

中央辺りにグラフの選択フォームが表示されているはずなので、この内「散布図」を選択し、左上の一番シンプルなサンプルを選択します。

そうすると出てくるのが次のような簡単なグラフです。
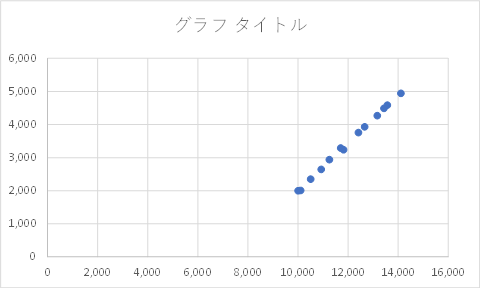
細かい書式の調整は省略します。
この後、点の部分を右クリックして表示される「近似曲線の書式設定」を選択します。
そうすると出てくるのが次の書式設定画面です。
次の内「線形近似」を選択し、また下の方にある「グラフに数式を表示する」をチェックします。
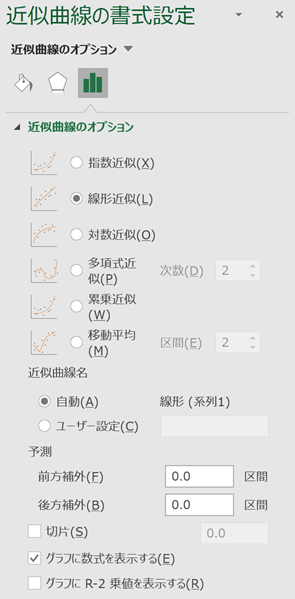
これにより、下記図のように数式が表示されます。
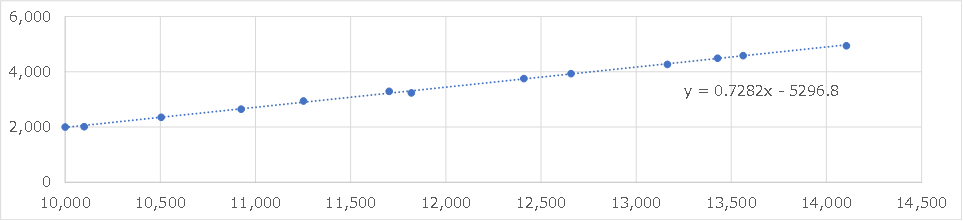
関数を用いて算出した傾き・切片と同じ数字ですね。
関数で出した数字のチェックに用いる事もできます。
このように、あくまでも簡便的な方法ですが、簡単に個変分解を行う事ができます。
サンプルExcelもダウンロードできるようにしているので、試してみて下さい。





コメント